Cuantificadores

Sabemos que las proposiciones afirman o niegan algo de un sujeto.

Dependiendo del sujeto, incluyen un cuantificador.

Ejemplifiquemos  y analicemos caso por caso:

     1)  Todos los números múltiplos de 2, son múltiplos de 4.

     2)  Todos los números múltiplos de 4 son múltiplos de 2.

     3)  Ningún entero par es divisible por 3.

     4)  Ningún número primo mayor que 2, es par.

     5)  Existe un natural, que satisface la ecuación .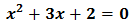

     6)  Existen naturales, que son la suma de sus divisores propios.

Universal y Existencial

En las proposiciones 1), 2), 3) y 4) se afirma algo sobre un todo.

Es decir, se afirma algo sobre todos los elementos de un cierto conjunto.

Por ello se dice que tales proposiciones incluyen un "cuantificador universal".

En cambio en las proposiciones 5) y 6) la afirmación es sobre alguien singular.

Por ello se dice que tales proposiciones incluyen un "cuantificador existencial".

Cuando son falsas

Reflexionando sobre la proposición 1), se puede descubrir que no todos los múltiplos de 2 son múltiplos de 4, es decir:

La proposición 1) es falsa porque "Existe un múltiplo de 2 (por ejemplo el 6), que no es múltiplo de 4".

Similarmente, reflexionando sobre la proposición 3), se pueden encontrar números pares divisibles por 3, es decir:

La proposición 3) es falsa porque "Existe un entero par (por ejemplo el 12), que si es divisible por 3".

Así mismo, resolviendo la ecuación dada en la proposición 5), se da uno cuenta que las soluciones no son naturales (), es decir:

La proposición 5) es falsa porque "Ninguna de las soluciones de la ecuación 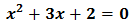, son naturales".

Cuando son verdaderas

Las proposiciones 2), 4) y 6) son verdaderas y por lo tanto requieren de demostración.

En este caso, son muy sencillas, pero las dejaremos para los ejemplos de demostraciones, más adelante.

Observación

Con cierta frecuencia, los cuantificadores en la proposiciones, no aparecen de manera explícita, por ejemplo:

La proposición 1) podría redactarse del siguiente modo:

Si x es múltiplo de 2, entonces x es múltiplo de 4.

Igualmente la proposición 5) podría redactarse del siguiente modo:

El conjunto solución de la ecuación 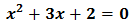, es subconjunto del conjunto de los números Naturales.