El método de Newton

Se trata de un procedimiento basado en la derivada, para encontrar aproximaciones a las raíces de una función real de variable real que sea derivable. Es muy útil en análisis numérico, sobre todo para aproximar raíces de polinomios en los cuales los métodos conocidos no funcionan (por ejemplo: 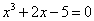, 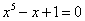) o para otro tipo de funciones, como por ejemplo: 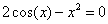o .

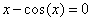Este método sirve inclusive para aproximar valores como por ejemplo: 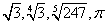, encontrando de manera aproximada las raíces de las siguientes ecuaciones 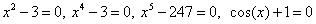, respectivamente.

No es un método infalible, pero más adelante explicaremos las condiciones para su eficiente funcionamiento.

Objetivo

Resolver algunos problemas sencillos de aproximación de raíces con el Método de Newton.

Conceptos previos

En economía, como en cualquiera otra disciplina, se suele describir la variación de una cantidad respecto a otra mediante:

• La derivada es la pendiente de la recta tangente a la gráfica de en .


• Por lo tanto la ecuación de la recta tangente a la gráfica de en es:

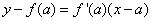, es decir: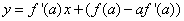

Descripción del Método de Newton

Sea 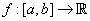una función derivable, de la cual sabemos que tiene una raíz en dicho intervalo y queremos encontrar una aproximación que nos satisfaga. ¿Qué hacemos?. Veamos:

• Elegimos 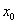en el eje de las x, asumiendo que está cerca de la solución de 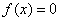(raíz buscada).


• Calculamos la ecuación punto pendiente de la recta tangente a la función en 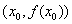, a saber:

(1)

• Esta recta debe intersecar al eje de las x, en un punto 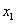, más cercano a la raíz buscada.


• Así, el punto 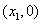satisface la ecuación (1) y sustituyendo, queda:

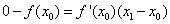(2)

• Si 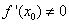, entonces, despejando 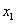en (2), queda que: .


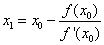• Repetimos el mismo razonamiento seguido para 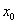, pero ahora comenzando con 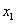, en cuyo caso obtenemos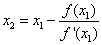, más cerca de la raíz buscada que .
  
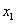• Iterando cada vez con el número obtenido, se construye una secuencia: 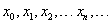de números cada vez más próximos a la raíz, tales que:

• La aproximación entonces será mejor, entre más términos querramos o podamos calcular.

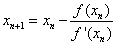
Nota

Debe ser claro que si alguna de las condiciones en los pasos anteriores falla, entonces el Método de Newton no puede funcionar.

Ejemplos

En los ejemplos se resuelven problemas sencillos de aproximaciones aplicando el Método de Newton.

Da clic en un ejemplo, ejecútalo y luego da clic en el botón de reiniciar

Al ver estos ejemplos, podrás pensar que es más fácil tomar una calculadora o cualquier
programa de computadora que haga los cálculos. En este caso, es importante pensar que
las calculadoras realizan sus cálculos, con base en métodos como el de Newton.

Ejercicios interactivos

En los ejercicios siguientes, se plantea la resolución de problemas de aproximación utilizando el Método de Newton. No olvides que debes tomar lápiz y papel para intentar resolverlos. Si deseas probar tus conocimientos, da clic sobre la siguiente imagen.